####NOTE: It is assumed below that are you are familiar with the basics of TensorFlow!
In November 2015, Google released TensorFlow (TF), “an open source software library for numerical computation using data flow graphs”. In sexier terms, TensorFlow is a distributed deep learning tool, and I decided to explore some of its features to see if it might be a precursor to SkyNet.
After looking through the tutorials provided by Google and the corresponding code, I felt the need to get more hands-on and implement a machine learning task myself. The goal for me was to start understanding the ins and outs of TF, not to push the boundaries of machine learning. So, in order to not reinvent the wheel, I began the task of creating a stacked autoencoder to predict handwritten digits using the MNIST database using TF’s python API. I closely followed the excellent tutorials at deeplearning.net, which uses Theano, another python deep learning library called.
The complete source code for this post as well as easy setup scripts so that you can run the MNIST training can be found on GitHub. The code will automatically download the dataset which consists of greyscale 28 x 28 pixel images of handwritten digits. The current version of code is tag v1.0. You can run the following to download the repo:
git clone https://github.com/cmgreen210/TensorFlowDeepAutoencoder
cd TensorFlowDeepAutoencoder
git checkout v1.0Our classification task is to predict the correct digit (0-9) from a 28 x 28 pixel image. Where do we start? The simplest possible thing to do would be to feed training images directly into 10 different logistic regression models (one for each class). These models would turn out to be very poor classifiers due to their simplicity. Another direction might be to create handmade filters in order to transform the input images into more useful forms. For example, we know that an 8 has to circular loops so we might have a ‘circular loop’ filter that would give a strong signal to an 8 but not a 1. This approach would require a lot of supervised handmade filters and would be susceptible to human bias and error.
What we really want is a method that can learn the important features of handwritten digits automatically in an unsupervised way. Once we’ve learned these features we can then apply a supervised “fine-tuning” step. Autoencoders precisely provide us with such a method.
Here I’ll briefly go into how we learn the aforementioned important features. For plenty of references and a detailed write-up check out Stacked Denoising Autoencoders.
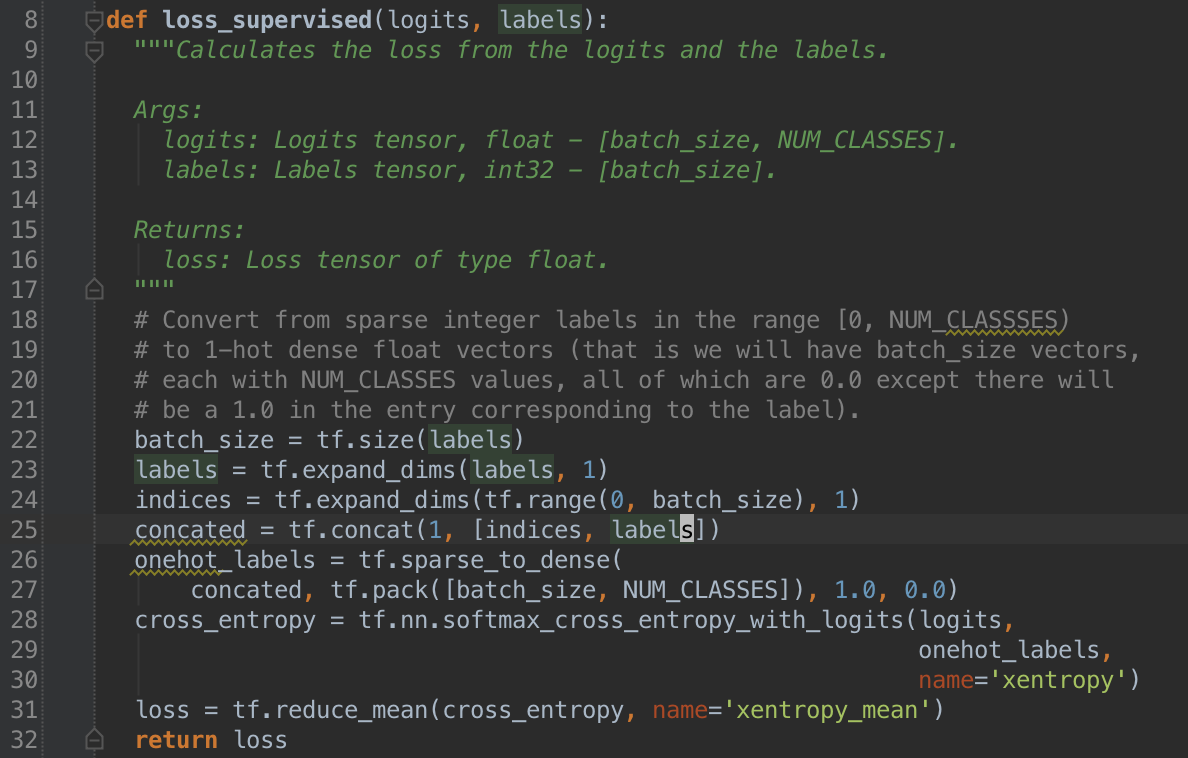
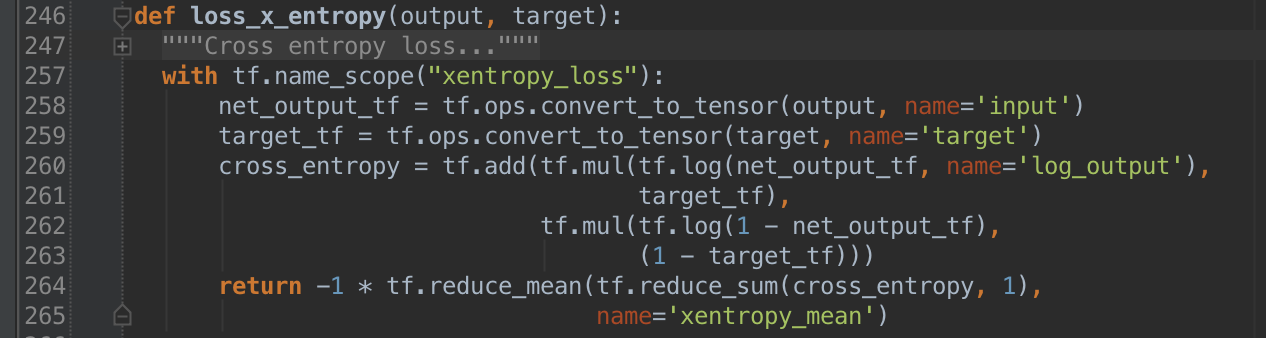
The idea is to feed an input vector, \(x\), whose elements have been scaled into \((0, 1)\), to a neural net with a single hidden layer whose output, \(z\), is as “close” to the input in the sense that we minimize the cross entropy between the two: \begin{equation} H(x, z) = - \sum_{k=1}^d[x_k\log{z_k} + (1-x_k)\log{(1 - z_k)}]. \label{eq:xentropy} \end{equation} Here we are interpreting \(x\) and \(z\) as probabilities, which allows us to use cross entropy (a concept from information theory) as a measure of similarity.
If you are concerned as to how we arrived at \(z\in[0,1]^d\) from \(x \in [0,1]^d\) here’s the formula: \begin{equation} z = \sigma(W^T\sigma(Wx + b_1) + b_2), \label{eq:net} \end{equation} where \(\sigma(s) = 1/(1 + e^{-s})\), \(W \in \mathbb{R}^{d\times m}\) (\(m\) being the number of neurons in the hidden layer), \(b_1\in\mathbb{R}^m\), and \(b_2\in\mathbb{R}^d\).
In TensorFlow we can implement cross entropy in a few lines with code that can be run on a single cpu, a single gpu, or even multiple gpus:
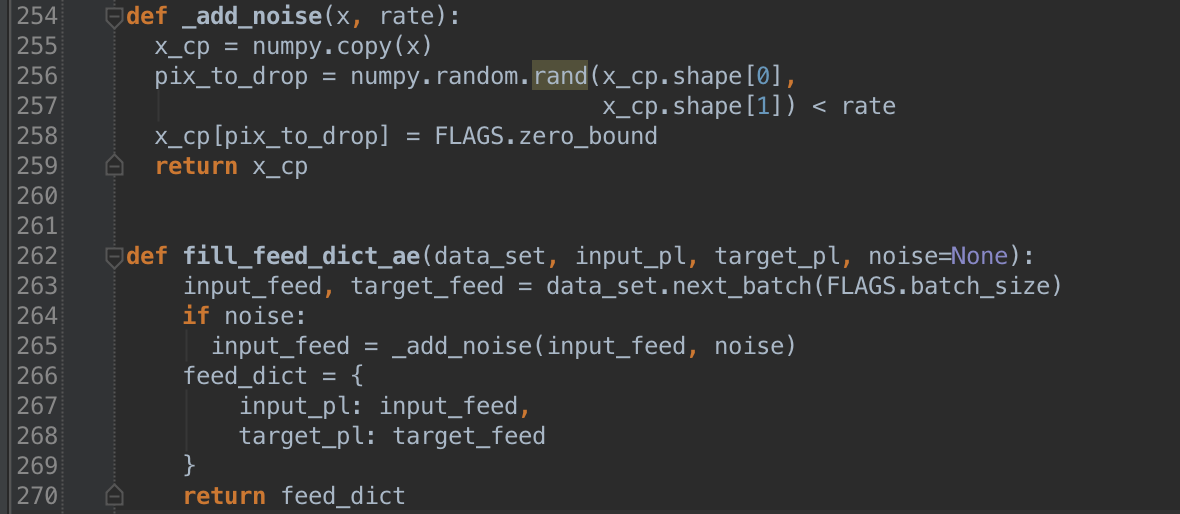
In this code example, we use 55,000 images to train our classifier. Of course, it would be nice to have more in order to ensure generalization beyond the training set. There are plenty of ways to accomplish this. Two of which being rotation and cropping of the images. Instead we’ll randomly distort the images by setting a percentage of pixels to 0. This allows our net to learn robust and generalized features by reconstructing distorted inputs.
Here’s how we accomplish adding noise:
Now to the stacked part of this post’s title. Neural nets can have multiple hidden layers (resulting in “deep networks”) that can learn more nuanced features. Furthermore, we can do the same pretraining routine for each hidden layer by first fixing the trained weights up to the current hidden layer and then using the output of this fixed sub-net as the input to our autoencoder training routine.
Implementing the stacking procedure with TensorFlow was one of the most challenging aspects of this exercise not because it was particularly complex but because it was easy to confuse trainable vs. non-trainable variables as well as keeping track of trained variables used to initialize the next layer weights.
The TensorFlow team has some tips on how to share variables during
training as well as helper functions, such as tf.get_variable(). However,
I found that it is very easy to forget which namespace/variable scope I’m in
at a particular instance of training. As a solution I chose an OOP approach
with the AutoEncoder class whose instances contain a TF variable dictionary
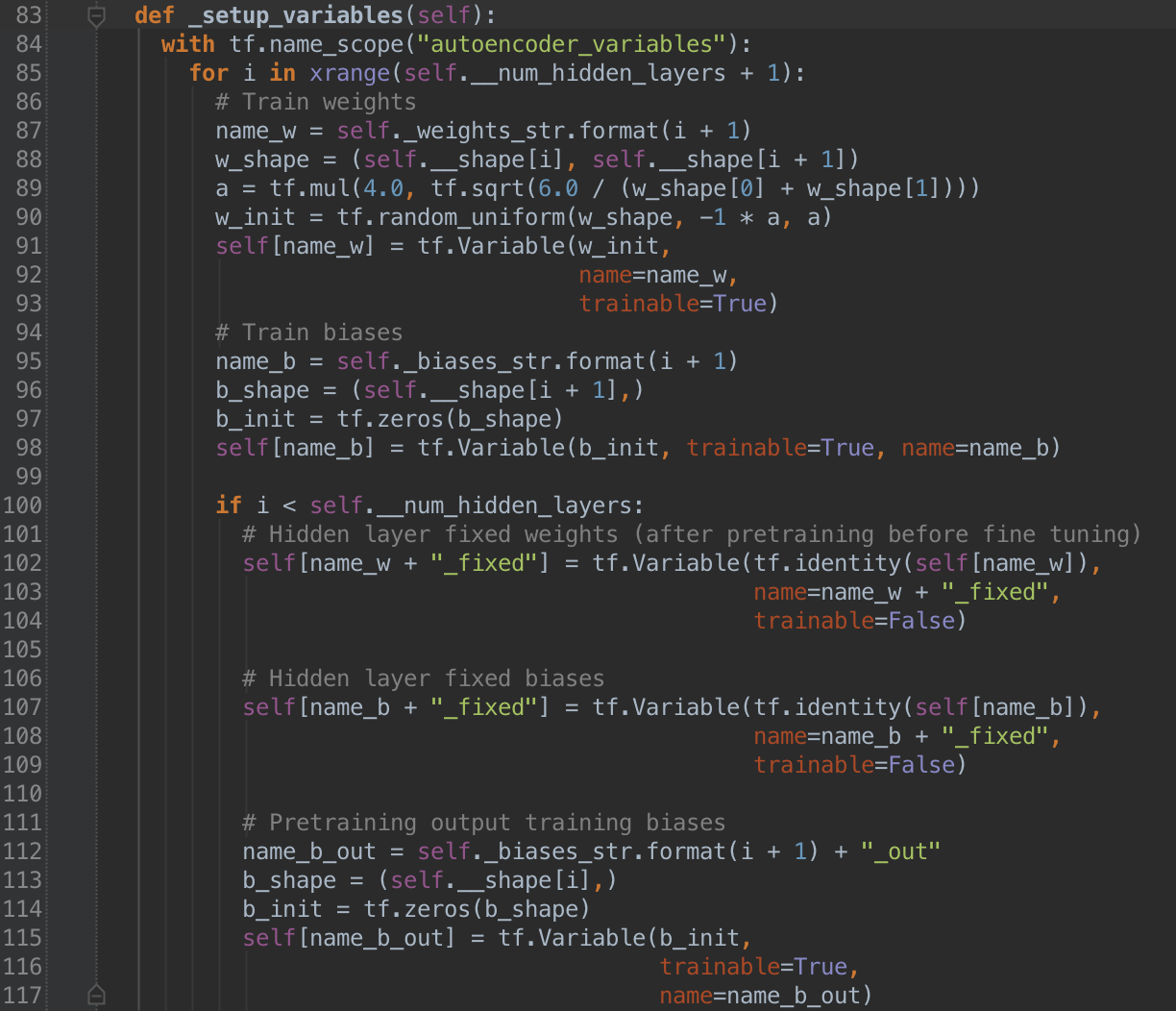
of each variable used in the network. Below is how we set up the TF variables
in the AutoEncoder class. Be sure to note which are trainable and how each
is initialized.
Now that we’ve completed unsupervised pretraining of our network we can move
onto the supervised stage. The variables are all initialized to their final
unsupervised values and are all trainable. The output of the network is 10
units each representing the probability of the input image being a particular
digit. For our error function we use tf.nn.softmax_cross_entropy_with_logits.
The python code we use for the error function is below.